Introduction:
Current models of Type Ia supernova favor the explosion beginning with a flame near the center of a white dwarf that accelerates as it moves outward due to various instabilities (Landau-Darrieus, Rayleigh Taylor). It is not known whether the burning front remains a subsonic flame, or if at some point, a detonation forms. The mechanism for a deflagration-detonation transition is not known, although several candidate models exist.
A flame propagates by balancing thermal diffusion and nuclear burning. Heat diffuses from hot ash to the cold fuel ahead of the burning front, raising its temperature to ignition. The width and speed of the burning front will depend on how rapidly energy is released from nuclear burning, and how efficiently conduction can transport energy to the material ahead of the front. For a typical white dwarf central density of 2 x 109 g cm-3 and a pure carbon environment, the flame thickness is 3.74 x 10-5 and the speed is 191 km/s (Timmes and Woosley 1992, hereafter TW). The radius of a white dwarf is ~ 1 x 108 cm, meaning a full simulation of a supernova will need to span 13 orders of magnitude spatially. As a first step in understanding Type Ia supernova mechanisms, we have begun to examine fully resolved thermonuclear flames using the FLASH code, and restrict ourselves to physics on the microscopic scales.
Numerical Method:
The FLASH code incorporates compressible hydrodynamics (using PPM), adaptive mesh refinement, a realistic equation of state (electron-positron, ions, and radiation), and a nucle ar burning module. To simulate a flame using the FLASH code, it was extended to incorporate energy transport. In the diffusion approximation, thermal transport can be expressed as a conductive heat flux:
where
s is the conductivity. This heat flux is coupled to the hydrodynamics in the energy equation:
|
In FLASH, this is accomplished by using operator splitting. The diffusion timescale is
|
where cv is the specific heat at constant volume / mass, and dx is the zone width. At the length scales necessary to resolve a flame (typically 10-5 cm to .1 cm), the diffusion timescale is typically several orders of magnitude larger than the CFL timescale, allowing us to use an explicit method for the conduction.
In FLASH, conduction is treated as a separate module. The heat flux is computed and added directly to the energy flux returned by the Riemann solver. These fluxes are then used to advance the cell average variables to the new time. Treating the heat flux this way ensures that the code remains conservative: whatever heat flux is added to one zone is subtracted from its neighbor.
To compute the heat flux, we use a conductivity module that treats the physics of white dwarf interiors (Timmes 1999), including the effects of electron-ion scattering, electron-electron interactions, and electron-phonon interactions in the degenerate regime. These conductivities are expressed as an equivalent opacity, and along with radiative opacities, are combined to form the total conductivity:
|
This module is called on a directly by the conduction module. Other conductivity routines, representing different physics can easily be substituted in place of the current one.
1-dimensional Carbon Flames:
The first test of these modules is reproducing the known 1-dimensional laminar flame speeds for white dwarf interiors. A table of these, used as a benchmark, was presented in TW. Here we consider only the pure carbon environments.
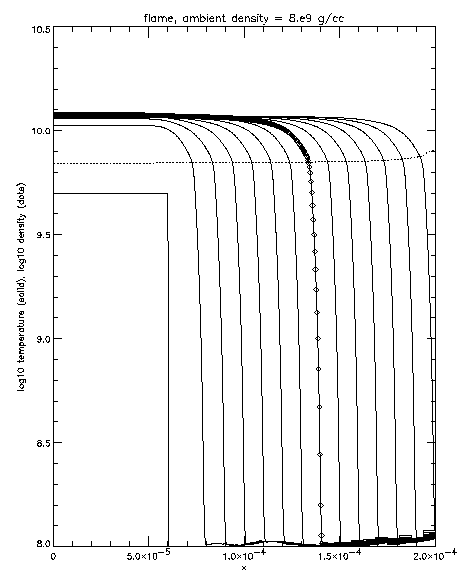
| Fig. 1: Pure Carbon Flame Evolution, r = 8 x 109 g cm-3. Solid lines show the temperature at different times, spaced 2 x 10-13 s apart. The grid spacing for this calculation was 3.9 x 10-7 cm, at the finest resolution, putting approximately 18 zones in a flame width. Diamonds on one temperature curve show the zones. The dotted line shows the density corresponding to the last temperature curve. |
To start the flame, the temperature in a small region of uniform density was raised to 5 x 109 K, at which point carbon burning will proceed rapidly. This sends out a pressure wave which quickly leaves the domain, leaving behind a hot region of ash. The energy released from the burning diffuses into the cold material ahead of the front, raising its temperature to ignition. This quickly enters a steady state, and a laminar flame front is formed. Figure 1 shows a flame front in a density of 8 x 109 g cm-3.
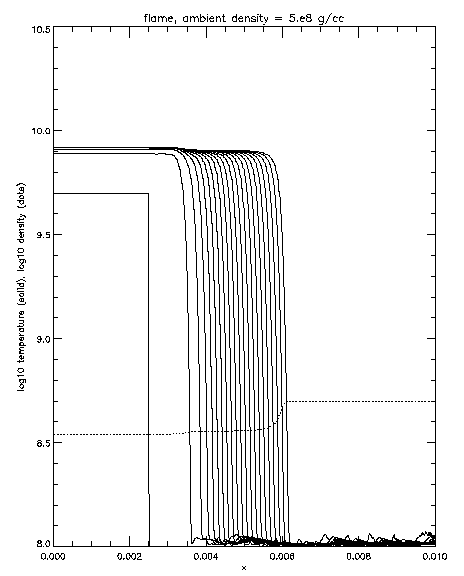
| Fig. 2: Pure Carbon Flame Evolution, r = 5 x 108 g cm-3. Solid lines show the temperature at different times, spaced 2 x 10-11 s apart. The grid spacing for this calculation was 9.8 x 10-6 cm, at the finest resolution, putting approximately 39 zones in a flame width. The dotted line shows the density corresponding to the last temperature curve. |
At this high density, we see the flame front is very steep and quickly moves across the domain. Note that the density falls behind the flame front. Figure 2 shows a flame front in a medium of density 5 x 108 g cm-3. Note that the domain is almost two orders of magnitude larger to accommodate the larger flame width. The density drop behind the front is larger for the low density case.
This comparison was done for many densities and the flame speeds were compared to those tabulated in TW. The comparison appears in figure 3.
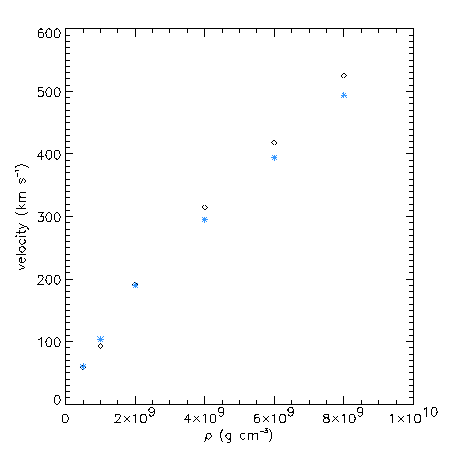
| Fig. 3: Comparison of flame speeds produced in FLASH (blue X) and those from TW (black diamonds) |
In general, the results from FLASH agree very well with those in TW. The largest difference in speeds is only 10%. Differences may be partially explained by the slightly different physics used in the two calculations. The TW results used a 130 isotope nuclear reaction network, while FLASH currently employs a 13 isotope a-chain network. As demonstrated in TW, the flame speed is sensitive to the nuclear reaction network size.
2-dimensional flames:
The thermal conduction module is extended to higher dimension via dimensional splitting, in the same manner as the current implementation of PPM. As a test of the diffusion in 2-dimensions, a flame with an initially circular perturbation was simulated with FLASH. After 10,000 timesteps, the burning front remained circular to the resolution of the calculation (see figure 4). This problem also illustrates the effectiveness of AMR at resolving the flame front.
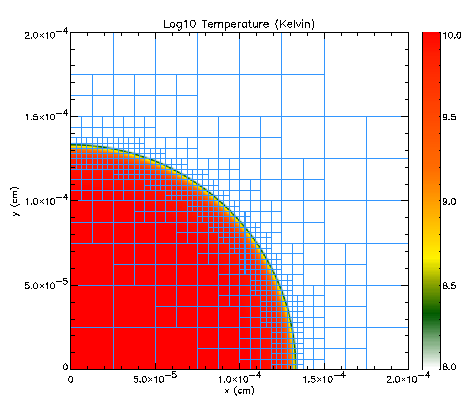
| Fig. 4: 2-dimensional circular flame front showing AMR refinement. |
Go back to Astrophysics Group Gallery page
Go back to main Flash Gallery page