Kinematic Translation Mechanism for Moderate-Sized Optics
A. I. Sheinis, J. E. Nelson, E. James, M. V. Radovan
Lick Observatory, University of California at Santa Cruz
1156 High St., Santa Cruz Ca. 95064
Phone: (831) 459-5095
Fax: (831) 459-4097
The Echellete Spectrograph and Imager (ESI), currently being completed for use at the cassegrain focus of the Keck II telescope, employs two moderate size translating fold mirrors. These mirrors are used to shift between the three instrument modes; medium resolution echellete mode; low resolution prismatic mode; and imaging mode. In order to maintain the optical stability and calibration of these three modes the mirrors must be removed and repeatably located to within 1.3 arcsecs of tip and tilt. In addition, the mirrors must maintain a fixed orientation relative to the telescope axis under a variety of gravity and thermal loads. In this paper we describe a novel concept for moving and locating these mirrors. Analytical analysis of the mounts is presented. Optical and mechanical testing is described.
Keywords: spectrograph, imager, echellette, Keck, kinematic, astronomy, translation
1. Introduction:
Extremely repeatable mirror positioning mechanisms are needed in the Echellette Spectrograph and Imager (ESI). ESI is a multipurpose instrument currently being delivered by the Instrument Development Laboratory of Lick Observatory for use at the Cassegrain focus of the Keck II telescope. The principle investigator for the instrument is Joe Miller, director of UCO/Lick Observatory. It is scheduled for first light on August 29, 1999. ESI is a medium resolution spectrograph, with a fixed 175.6 line/mm echellette grating and two large (25 kg) cross dispersion prisms. The instrument also contains an off-axis, ellipsoid collimator and an f/1.07, all-sperical, 10 element refracting camera. ESI is described and referenced in detail in a previous paper by Epps and Miller1.
The spectrograph is designed to accommodate the (0.39 to 1.10)-micron pass-band without refocus over an operating temperature range of û4° C to +6° C. The spectrum is detected by a single flat (2048 by 4096 by 15-micron) thinned, back-illuminated, MIT-Lincoln Labs CCD. The entire spectrum is recorded in a single exposure for both the echellette and the low dispersion prismatic (LD) modes. The echellette mode accommodates a 20 arcsec-long slit and has a resolution (l /D l ) of approximately 26,087 per pixel. The LD mode takes spectra from up to 50 objects or along a single 8 arcmin long slit at a per-pixel resolution of 4839 (at .39 microns) to 1052 (at 0.80 microns). The imaging mode covers a 2 by 8 arcmin field of view at 0.153 arcsecs per pixel.
ESI currently has three scientific modes available: a medium resolution Echellete mode: a low resolution prismatic mode, and an imaging mode. To switch between these modes ESI employs two moderate size (10kg) translating fold mirrors, which must reapeatably locate in angle and position. A novel locating mechanism has been designed to achieve this reapeatability for these mirrors. It is this mechanisms which moves and locates these two mode changing mirrors that we discuss in the following paper
The different modes are selected as follows; Light from the Cassegrain image (Figure 1) at the slit plane is collimated by an off-axis segment of an ellipsoid. The collimated light first passes through the pre-dispersing prism, then to the grating, then back through the pre-dispersing prism a second time and on to the post-dispersing prism. In this way the echellette spectrum is dispersed by a single reflection at the grating and cross-dispersed by the two prisms. In order to create the multi-object, low-dispersion mode, a mirror is placed in between the predispersing prism and the grating. In this way, light is directed back through the two prisms and into the camera, dispersed only by the prism and not the grating. The imaging mode is created by placing a mirror in front of the pre-dispersion prism, to steer it straight into the camera, thus the light is not dispersed at all.
2. Requirements
In order to enable the use of a single set of standard reference spectra and flat field data between different exposures, the scientific requirements for the spectrograph are such that the spectra move by no more than 0.038 arcsecs on the sky (0.25 pixels) in switching between modes. This places a 1.3 arcsec allowable tip/tilt repeat accuracy on the low dispersion mode fold mirror (LDM). A similar requirement was adopted for the imaging mode fold mirror (IM). In addition, the packaging constraints left little space for a conventional translation stage for either mirror.
Given these two sets of requirements , we determined that a conventional translation stage could not be used, so we set out to design something new.
3. Opto-mechanical Design
The mechanical system is pictured in Figures 2, 3a and 3b. Three V-blocks containing six kinematic locating planes are rigidly mounted to nodes within the optical sub-structure. The nodes are determined by the intersection point of two or more structural plates. Three tooling ball assemblies are bonded to the zerodur mirror substrate via Invar pads. The bonding process is identical to that described previously 3,4 for other assemblies in this spectrograph. The locating-concept is based on a soft-mounted mirror whose orientation is flexible with respect to the mount. The mirror is located by driving the mount in such a way that the three tooling balls contact all six locating surfaces. The goal is to get the tooling balls to locate in the V-blocks (which can require a considerable amount of force), while minimizing the amount of residual stress within the mirror.
This is achieved by mounting the mirror, on springs, to a frame. The springs are attached between the invar pads and the frame such that the lines of force pass directly through the invar pad and glue film when the mirror is in the parked position. This puts the glue, glass and invar in tension in the parked position. The tension forces are spread out over a large glue contact area, keeping the stress well below maximum acceptable levels. When the frame is driven towards the in position, the tooling balls contact the v-blocks (typically individually). The balls slide along the v-blocks until all six surfaces are contacted. As the balls contact the V-blocks, the forward 4 springs elongate, increasing the force on the balls. At the same time the rear two springs contract, reducing the amount of force passing through the glass. In this way, the full tension force can be applied to the kinematics, while having zero force transmitted through the glass (neglecting friction).
The frame has very loose tilt tolerances (of order several degrees), because it does not affect the mirror location as long as the V-blocks contact. This loose tolerance allows a great deal of flexibility in designing a slide mechanism. We cantilever the frame on very small crossed roller slides in order to package the slide mechanism.
The linear position accuracy required of the frame is fairly tight, to accurately control the amount of spring compression. To achieve the tight positioning accuracy, we use an encoded stepper driven ball-slide to drive the frame.
3.1 Friction Analysis
In order to predict the viability of this design configuration we undertook an analysis of the friction forces at each ball-kinematic contact surface. In a mechanism such as this, it is critical that the 6 defining surfaces are contacted cleanly. If the mechanism stops with only 3 or 4 or 5 surfaces contacted, the mirror position will be ill-defined; and no amount of increased driving force will cause the mechanism to engage the other defining points. This is because the opposing forces at the surfaces are proportional to the normal force, which in turn is proportional to the driving force. Thus, for a given coefficient of friction, the success of the mechanism is a function only of the geometry and not the driving mechanism. We now examine the frictional contribution at each of the contacting surfaces. Surface geometry is shown in Figure 2.
The following analysis is based on treating the mirror as a free-body. We consider the case of 3, 4 and 5 surface contact. In each case we calculate the critical coefficient of friction required for static equilibrium. Note that we will not calculate the critical condition for a 1 or 2 surface contact, since in this design, the opposing force at these surfaces is not proportional to the driving force due to the application of an out-of-plane spring (see Figure 2). For this case only, we can increase the driving force to overcome the resistive force.
3.1.1 Three surface contact
For three surface contact, the mechanism will be sliding on surfaces one and two. It will then contact any of the other three surfaces. The critical coefficient of friction required to stop the mechanism, in this case is given by
![]()
Where b 1 is the opening half-angle of the V-block and d is the angle between the motion of the mirror and the in-plane component of the normal force.
3.1.2 Four surface contact
For 4 surface contact, surfaces 1-4 are contacted. The mirror rotates about point "c" because it is constrained to move tangent to a circle at blocks one and two. The critical coefficient of friction required to stop the mechanism for the case of four-surface contact is then given by:
![]()
Where b 1 is again the opening angle and b is the angle between the in plane component of the normal force and the line between balls 1 and 2.
3.1.3 Five surface contact
For 5 surface contact, surfaces 1-4 are contacted. Again, the mirror rotates about point "c" because it is constrained at blocks one and two. The mirror then contacts one of the two remaining surfaces The critical condition for five point contact is given by:
![]()
Where,
![]()
b , b 1 and d are defined as above.
We have used these relations to estimate the maximum acceptable coefficient of static friction for each case. One can take the analysis a step further and use the relations to calculate the geometry required to give a single critical friction coefficient for all cases, and then optimize this geometry for a maximum coefficient of friction.
3.2 Repeatability analysis
Non-repeatability in the angular location of the optics can be attributed primarily to three factors: 1) compression of the ball/kinematic flat due to Hertzian contact stress; 2) bending of the invar glue pad assemblies; and 3) deformation of the glass optic itself. In order to estimate the repeatability of the device we calculate the magnitude of each of these effects.
3.2.1 Hertzian contact stress
The maximum normal force (ignoring friction) at each surface for this geometry can be shown to be:
![]()
Where F = driving force, d = angle of the V-block normal in the mirror and b 1 = the opening half-angle of the kinematic V-block.
In this assembly we chose a driving force equal to the weight of the mirror, giving a variation in the normal force with gravity of +/- mg/2.65.
Hertzian contact stress and deflection for a ball on a plane are given by7:
![]()
![]()
![]()
![]()
Where a and b are the major and minor axes of the contact ellipse, R is an average contact ellipse radius, F is the normal force, f is the force applied to the mirror and
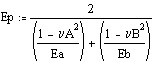
![]()
![]()
![]()
![]()
![]() .
.
![]() PSI
PSI ![]() inches
inches
![]() PSI
PSI ![]() inches
inches
Where Rb = ball radius, Ra = flat radius (infinity); Ea, Eb and n A, n B are Youngs modulus and Poissons ratio for both materials.
From the above analysis and given the driving force of twice the mirror weight, and our geometry, the maximum hertzian contact stress is 144,000 PSI. For the variation in normal force given above, the maximum change compression per kinematic is 1.4 microns. This corresponds to an angular error of 0.96 arc seconds for our system geometry.
In addition, with such a high contact stress, we needed to be very concerned about material selection, so as not to yield the material. We chose Speedstar AISI type M2 (UNS T11302) high speed steel, hardened to Rockwell 62, with a yield stress of over 400,000 PSI, for the kinematic v-blocks. Also, we used hardened (SS 1142) tooling balls for the locating balls that were hardened to Rockwell 60, with a yield stress of 285,000 PSI.
3.2.2 Mirror and Mount Deformation
Deformation of the Invar glue pad assembly was modeled as a simple cantilevered beam. This deflection was found to be more than two orders of magnitude below the above effect.
In order to estimate deflection of the mirror due to a three-point support, we relied on the analysis of Nelson et al5. The rms deflection of the mirror is given by:
![]()
Where x rms = the support efficiency, A = mirror area and q = applied pressure to the plate. The support efficiency for a 3 point radial support at the edge is 24.7 x 10-4. The modulus of rigidity, D is given by:
![]()
We used these two equations with a mirror radii = 130 mm, thickness = 45 mm for the IM and 25 mm for the LDM, and Poissons ratio of .3 and Youngs modulus of 9 x 1010 N/m2 for Zerodur. This resulted in a calculated rms deflection of .026 microns or l /40 (at .633 microns) for the IM and a calculated rms deflection of 0.15 microns, or l /6 for the LDM.
4. Bench Testing and Performance Analysis
In order to test the system it was assembled prior to the rest of the spectrograph. An interferometer was used to measure the deformation of the mirror and the repeat accuracy of the system. With this technique, no visible deformation was observed in the mirror (to l /10), and the repeat accuracy was observed to be better than 1 arcsecond in a single gravity orientation.
Once the entire spectrograph was assembled, we were able to make repeatability measurements in situ. This was done by placing a machined pinhole in the slit plane to create an artificial star. Using a calibration line lamp, the image position on the CCD was recorded all three modes both before and after the individual mirrors were engaged for a single orientation of gravity. Next, the spectrograph was mounted in a cassegrain simulator, which allowed us to tilt it, thereby inducing the different gravity orientations the spectrograph would see at Keck. We again tested the repeatability of the both stages and determined them to be sub arcsecond in all gravity orientations. An issue was identified with one of the stages at a single gravity orientation. The simple solution for now is not to change modes in that gravity orientation. This issue will be addressed during commissioning.
5. Conclusion:
We have described the design of a kinematic positioning system for moderate sized optics. The system relies on the optic cleanly contacting three v-blocks containing six surfaces. The optic is delivered to the V-blocks via a spring loaded mount. We have analyzed the design from the standpoint of friction, beading and surface deformation. We have presented test results showing an a repeatability below 1.3 arcseconds of tip/tilt. The system is currently built and resides in ESI at the Keck Observatory on Mauna Kea.
The authors wish to thank Carol Osborne and Mary Poteete for their help with the design drafting and many of the Figures for this paper. Also, we would like to thank Jeff Lewis and Jack Osborne for their many helpful comments;
7. Bibliography: