107 K
Q. Is there any place in the sun where the temperature is high enough for
nuclear fusion to take place?
This is an excellent question. We know the temperature at the surface
of the Sun is far too cool for fusion. What about as we go deeper towards
the center? This is the subject of a topic called Stellar Structure.
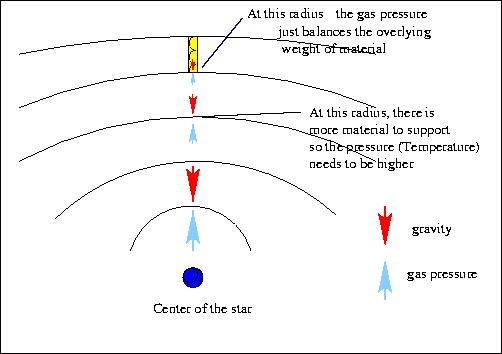
It's all based on the concept of HYDROSTATIC EQUILIBRIUM - the downward force due to gravity (i.e the weight) of the gas must be balanced by the upward thermal pressure of the gas. If these forces were not equal, the star would be collapsing inward or expanding outward.
The pressure exerted by a gas increases as the temperature of the gas increases. If you think about a container filled with gas atoms or molecules, the thermal pressure exerted on the walls of the container is due to all the atoms and molecules bouncing off the walls. Remember, temperature is a measure of the mean kinetic energy of the gas particles.
At each level moving down towards the center of the Sun, the total column of mass above every point increases, so the Gravitational Pressure increases as you move in from the surface of the Sun. To maintain Hydrostatic Equilibrium, the Thermal Pressure must also increase with depth which requires that the temperature increase toward the center of the Sun.
With computers it is possible to build (we think) very accurate models of the Sun and other stars based on the the requirement of hydrostatic equilibrium and the laws of chemistry and physics. We can predict the temperature and density of the Sun at each radius from the center to the surface.
You can see that the temperature at the center of the sun (T = 1.5 x 107 K) is much greater than the temperature at the surface of the sun (T = 5800K). The central temperature of the sun is definitely high enough for nuclear fusion to take place there. Actually the temperature is high enough that fusion can take place in the inner 10% of the sun.
A. -rays are realeased during the P-P fusion chain and almost immediately (after traveling on average 1 cm) absorbed and re-emitted. The energy contained in that original -ray bounces its way outward, and after ~100,000 years and 1022 absorptions and re-emissions, it leaves the surface of the Sun "downgraded" into visible light photons (because of the temperature gradient in the Sun).
How Much?
| 4 x 1033 ergs/sec x | 1 |
= 6.25 x 10 14 grams/sec |
| 6.4 x 1018 ergs/gram |
Q. A more massive star has a higher or lower central temperature?
A. Higher of course - hydrostatic equilibrium demands this.
The P-P Chain reation rate increases (steeply) with temperature. A higher central temperature means the P-P rate is higher and more energy is released - this means a larger luminosity.
So more massive stars have higher central temperatures which results in higher P-P rates which releases more energy and causes the star to have a higher luminosity. So for stars on the main sequence, more massive stars = higher luminosities
He .
We calculated the lifetime of the Sun as an H-fusion-powered object, but this assumed the entire Sun was pure Hydrogen and that ALL the hydrogen could be fused to Helium. In fact, by the time that about 10% of the Hydrogen is fused to Helium the Sun will change its structure and will no longer be a main-sequence star.
A 10 M
has a central temperature of
30,000,000 K and a luminosity of 40,000
L .
We know that the fuel of stars is mass and that the
rate of fuel consumption is the luminosity. So the
10 M star would be expected to live 10 times
longer based on its extra fuel, but, 1/40000 less long based on its fuel
consumption:
| Lifespan ( 10 M ) |
= | 10 |
x | Lifespan ( 1 M ) |
= | 0.00025 x Lifespan ( 1 M ) |
| 40,000 |
Similarly a 0.3 M star with
0.01 L would have a main-sequence
lifetime that was:
| Lifespan ( 0.3 M ) |
= | 0.3 |
x | Lifespan ( 1 M ) |
= | 30 x Lifespan ( 1 M ) |
| 1/100 |
So even though more massive stars have more fuel (mass),
they use it up faster (higher luminosity) and so have shorter main sequence
lifetimes than the less massive stars.
Michael Bolte 
