DISTANCES TO STARS

It is crucial to be able to measure the distances to stars if we are to derive intrinsic luminosities. There are several methods for measuring distances to stars, but the most reliable by far (when it can be applied) is Trigonometric Parallax.

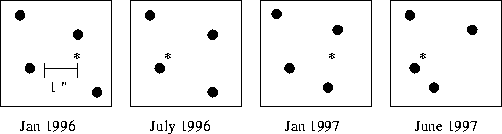
An experiment: Hold a finger up in front of your nose, close one eye and note where the finger appears on the back wall. Now close the other eye (and open the one that was closed before) and note that the finger appears to move on the back wall. If you do this same experiment now holding the finger at arm's length, you will notice that the apparent motion of the finger against the background is smaller (unless you have really short arms). These are examples of the parallax effect - the apparent motion of a nearby object compared to distance background objects because of a change in viewing angle.

• For nearby stars we also measure a parallax - an apparent annual motion of the stars compared to background stars that is really a reflection of the Earth's motion around the Sun. This is illustrated in the figure below. The asterick is a nearby star which is apparently moving back and forth every year compared to the more distant background stars. (Note the star at the lower right which has a proper motion).
  

  
  

• Here is another view of trigonometric parallax for stars observed as the Earth orbits around the sun:
  

  The distance to the star is inversely proportional to the parallax angle (which is usually indicated by the symbol )

  
  
  

Parsecs and Arcseconds

• There is a special unit of distance called a parsec.
  A star whose annual parallax angle is 1 arcsecond is is at a distance of 1 parsec.

  What is an arcsecond ( )?

  

  So	1   =	1	x	1	x	1	=	1	of a circle
  		60		60		360		1,296,000

  
  

  This is the angular size of a dime seen from 2 miles away!

  The distance to a star in parsecs is:   d =	1	when is measured in arcseconds.

Nearby stars

• How far away ARE the nearby stars? The closest star (aside from the Sun) is called Proxima Centauri with a parallax of 0.77 . This means it is more than 1 pc away:
  

  d (pc)   =	1	=	1	=   1.3 parsecs
  			0.77

• Even the largest parallax (that for the closest star) is small. The atmosphere blurs stellar images to around 0.08   so "astrometrists" are trying to measure a tiny motion of the centroid of a stellar image as it moves back and forth every six months. In the previous diagrams the parallax motions have been greatly exaggerated.

• From the ground it is possible to measure parallaxes for stars out to around 80 pc -- this corresponds to very tiny motions.

  d =	1			=	1
  					d

  So, a star at 80 pc has a parallax angle of only	1	=   0.0125 arcsec.
  	80

• Within a sphere with a radius of 10 LY (3 pc) there are only 10 known stars:
  

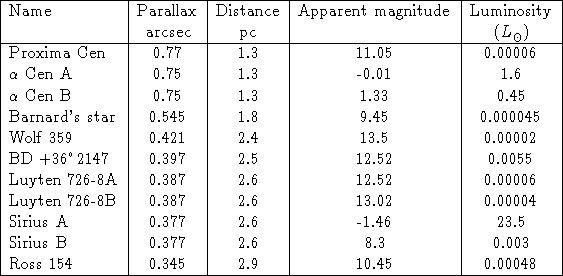
  (Note that most of the nearest stars are faint in apparent brightness and much less luminous that the Sun.)